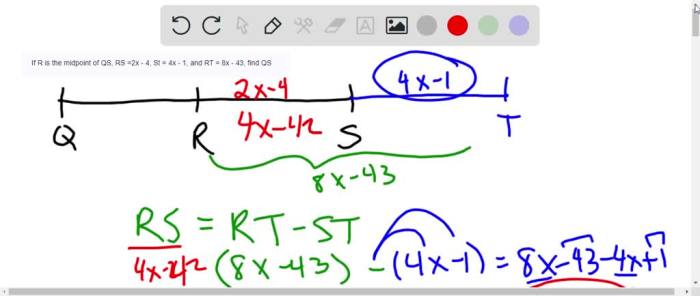
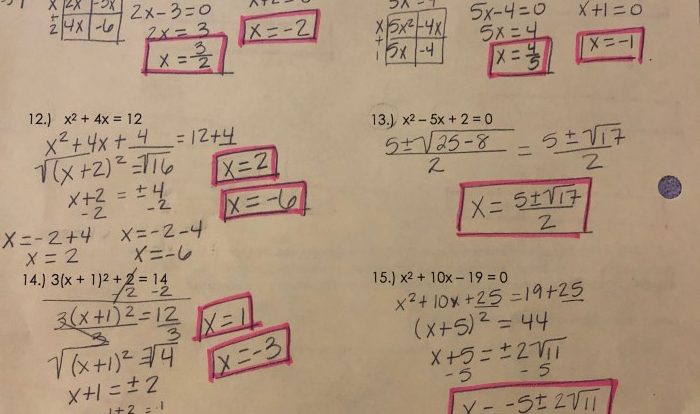R is the midpoint of QS, a fundamental concept in geometry that holds significant importance in various applications. Join us as we delve into the intricacies of midpoints, exploring their definitions, geometric properties, and practical applications across diverse fields.
From determining the center of a segment to understanding the motion of objects, the midpoint formula serves as a crucial tool in both theoretical and practical domains. Let’s embark on a journey to unravel the significance of r as the midpoint of qs.
Definitions
Before diving into the topic, let’s clarify some essential terms:
Midpoint
The midpoint of a line segment is a unique point that divides the segment into two equal parts. It is the point at which the segment is balanced, with equal distances to both endpoints.
Segment
A segment is a part of a line that has two distinct endpoints. It is a straight path connecting two points, with no other points lying on the line between them.
Relationship between Midpoint and Endpoints
The midpoint of a segment is always located exactly halfway between the endpoints. It is the average of the coordinates of the endpoints. This means that the distance from the midpoint to each endpoint is equal.
Applications
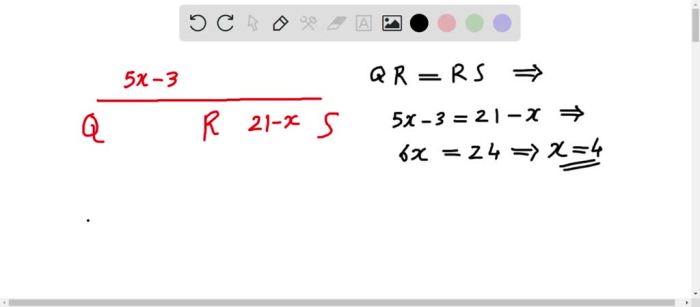
The midpoint formula is a versatile tool with numerous practical applications in various fields.
One fundamental application of the midpoint formula is determining the center of a line segment. By calculating the midpoint of two given endpoints, we can locate the exact middle point of the segment, which is often crucial for geometrical constructions, measurements, and design.
Knowing that r is the midpoint of qs is crucial for understanding the concept of segment addition in geometry. If you’re looking for a comprehensive guide on oral mech exam write up, I highly recommend checking out this article: oral mech exam write up . It provides a step-by-step approach to effectively prepare for and complete an oral mech exam.
Returning to our topic, the midpoint formula can be applied to find the midpoint of any line segment, including qs, given the coordinates of its endpoints.
Real-World Applications
- In architecture and construction, finding the midpoint of a segment is essential for ensuring symmetry, balance, and proper alignment of structures and components.
- In engineering, the midpoint formula is used to determine the center of mass or gravity of objects, which is crucial for stability and performance calculations.
- In navigation and surveying, the midpoint formula helps determine the midpoint of a line connecting two points on a map or chart, aiding in accurate distance measurements and route planning.
Additionally, the midpoint formula is instrumental in dividing a segment into equal parts. By finding the midpoint and then using it as a reference point, we can divide the segment into two equal halves or into multiple equal parts as needed.
Geometric Properties: R Is The Midpoint Of Qs

The midpoint of a segment possesses several key geometric properties that govern its relationship with the segment itself and its perpendicular bisector.
Congruent Segments
The midpoint divides the segment into two congruent segments. This means that the two segments formed by the midpoint have the same length. Let’s denote the segment as PQ and its midpoint as R. Then, the length of PR is equal to the length of RQ.
Perpendicular Bisector
The midpoint of a segment lies on the perpendicular bisector of that segment. The perpendicular bisector is a line that passes through the midpoint and is perpendicular to the segment. It divides the segment into two congruent halves, creating a right angle at the midpoint.
Coordinates

In coordinate geometry, the midpoint of a segment is a crucial concept that allows us to determine the exact location of its center point. By utilizing the coordinates of the segment’s endpoints, we can effortlessly calculate the coordinates of its midpoint.
Finding the Coordinates of the Midpoint
To find the coordinates of the midpoint of a segment with endpoints (x1, y1) and (x2, y2), we employ the following formula:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
This formula essentially computes the average of the x-coordinates and the average of the y-coordinates of the endpoints, resulting in the coordinates of the midpoint.
Examples
- For the segment with endpoints (2, 3) and (6, 9), the midpoint is ((2 + 6) / 2, (3 + 9) / 2) = (4, 6).
- For the segment with endpoints (-3, 5) and (1, 1), the midpoint is ((-3 + 1) / 2, (5 + 1) / 2) = (-1, 3).
Significance in Coordinate Geometry, R is the midpoint of qs
The midpoint formula is a fundamental tool in coordinate geometry, enabling us to:
- Determine the center point of a segment, which is particularly useful in geometric constructions.
- Bisect a segment, dividing it into two equal parts.
- Solve problems involving the distance between points and lines.
Applications in Physics
The concept of midpoint is widely used in physics to understand various phenomena and solve problems related to motion, balance, and stability of objects.
Locating the Center of Mass
In physics, the center of mass of an object is the point where the entire mass of the object can be considered to be concentrated. Finding the midpoint is crucial for locating the center of mass, which is essential for understanding the object’s motion and behavior under external forces.
Balancing Objects
The midpoint also plays a vital role in balancing objects. When an object is balanced on a point or line, the midpoint of the object must be directly above the point or line of support. This principle is used in various applications, such as balancing toys, designing stable structures, and maintaining equilibrium in physical systems.
Motion of Objects
The midpoint of an object can also provide insights into its motion. For example, in the case of rotational motion, the midpoint serves as the axis of rotation. Understanding the midpoint’s role in motion helps analyze and predict the trajectory and behavior of objects.
Advanced Concepts
In higher dimensions, the concept of the midpoint generalizes naturally. For instance, in three dimensions, the midpoint of a line segment joining two points $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ is given by$$\left(\fracx_1+x_22, \fracy_1+y_22, \fracz_1+z_22\right).$$This formula can be extended to any number of dimensions.
Centroid
The centroid of a geometric figure is a generalization of the midpoint. It is the point that represents the “center of mass” of the figure. For a triangle, the centroid is the intersection of the medians (lines connecting the vertices to the midpoints of the opposite sides).
For a tetrahedron, the centroid is the intersection of the medians of the four faces. In general, the centroid of an $n$-dimensional figure is the point whose coordinates are the arithmetic means of the coordinates of the vertices.The centroid has several important properties.
For instance, it is the point that minimizes the sum of the squared distances to all the vertices of the figure. It is also the point that minimizes the potential energy of a system of point masses placed at the vertices of the figure.
Applications in Calculus and Other Advanced Mathematical Fields
The midpoint formula and the concept of the centroid have numerous applications in calculus and other advanced mathematical fields. For instance, the midpoint formula is used to find the average value of a function over an interval. The centroid is used to find the center of mass of a region or a solid.The
midpoint formula and the concept of the centroid are also used in physics to find the center of mass of objects and to calculate moments of inertia.
User Queries
What is the definition of a midpoint?
A midpoint is a point that divides a segment into two equal parts.
How do I find the coordinates of the midpoint of a segment?
To find the coordinates of the midpoint, add the x-coordinates of the endpoints and divide by 2. Do the same for the y-coordinates.
What are some real-world applications of finding the midpoint?
Finding the midpoint is essential in various applications, such as determining the center of a circle, balancing objects, and understanding the motion of projectiles.